Alle bisher bekannten und angewendeten Systeme der Mannschaftskämpfe haben als Ziel den Sieg der eigenen Mannschaft. Das Ergebnis berücksichtigt in der Regel nicht die Leistung des einzelnen Teilnehmers. Es werden zwar mitunter intuitiv Ehrungen für „der beste Sportler/Spieler“ oder „die beste Sportlerin/Spielerin“ als Journalisten-Auswahl vergeben. Ansonsten sind manchmal die Titel „player oft the match“ oder verschiedene Ehrungsmedaillen für individuelle Einzelleistungen bekannt. Mit einem mathematischen Nachweis sind diese individuellen Auszeichnungen aber nicht hinterlegt.
Ein Beispiel zur Relation der Einzel- und Mannschafts-Ergebnisse im Sport:
1.Tischtennis-Weltmeisterschaft, Wettbewerb im Doppel
Das Team „Deutschland“ mit den Spielern GER1 und GER2 spielt im Finale der Tischtennis-Weltmeisterschaft gegen die chinesische Mannschaft CHN1 und CHN2.
Angenommen die Chinesen gewinnen und sind Weltmeister!
Aber das ist ja das gesellschaftliche Ergebnis, nicht das mathematische!
Denn wenn GER1 und CHN1 gegen GER2 und CHN2 spielen würden oder GER1 und CHN2 gegen GER2 und CHN1 spielen, dann kann durchaus ein anderes Team Erfolg haben, nämlich eines, dass den nationalen Zwängen, der heute üblichen gesellschaftlichen Zuordnungen nicht untersteht. Also muss das rechnerische Ergebnis der Weltmeisterschaft mit dem gesellschaftlichen Ergebnis nicht unbedingt identisch sein.
Die „Wahrheit“ des stärksten Teams lässt sich erst in drei Spielen ermitteln:
GER1+GER2 ⇔ CHN1+CHN2;
GER1+CHN1 ⇔ GER2+CHN2;
GER1+CHN2 ⇔ GER2+CHN1
Ländervergleich
Das Ergebnis kann z. B. so:
CHN1 und CHN2 auf dem obersten Treppchen
GER1 und GER2 – erreichen den 2. Platz
oder so aussehen:
CHN1 und GER1 auf dem oberstenTreppchen
CHN2 und GER2 – erreichen den 2. Platz

WM-Ergebnis
Ein Tischtennis-Doppel-Kurzturnier aus vier Teilnehmer (Nr. A bis Nr. D) beinhaltet drei Spielrunden mit bis zu drei Gewinnsätzen und könnte beim Partnerwechsel in den Teams im Rotationsprinzip mathematisch korrekt z. B. so verlaufen:
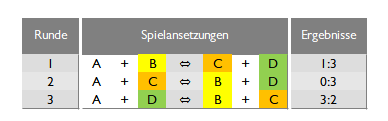
Teilnehmende Spieler A, B, C, D
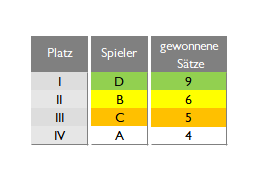
– Farben in allen Tabellen: Platz 1 = grün, Platz 2 = gelb, Platz 3 = orange
– Satzende bei 11 Punkten oder mehr (beim Stand 10:10)
Wenn ein Spielsatz etwa 10 bis 12 Minuten dauert, dann ist ein Kleinturnier im Beispiel oben mit 9–15 Sätzen in 90 bis 180 Minuten bzw. in etwa zwei bis vier Stunden beendet, wenn man Pausen von ungefähr 10 Minuten mitrechnet. Eine angemessene Zeit für einen interessanten Wettkampf!


Grundgedanke der Idee ist eine Einzelbewertung der Teilnehmer eines Turniers. Es wird ein Wettbewerb für Einzelpersonen/Einzelteilnehmer im Rahmen eines Teamturniers durchgeführt, der sich durch Rotation der Teilnehmer in der Mannschafts-Zusammensetzung auszeichnet. Die Ergebnisse der jeweiligen Mannschaft werden den einzelnen Teilnehmern dieses Teams zugeordnet – jeder erhält die der Mannschaft zugehörigen Punkte, Tore, Wertungen als eigenes Guthaben.
Der Spieler Nr. D hat alle drei Runden für sich entschieden und dabei insgesamt neun Sätze gewonnen. Für ihn ergibt sich ein eindeutiger 1. Platz.
Den Kampf um Platz 2 hat der Spieler Nr. B knapp vor dem Spieler Nr. C mit dem Sieg in der 2. Runde und insgesamt sechs gewonnenen Sätzen für sich entschieden. Leider hat der Spieler Nr. C mit dem Sieg in der 1. Runde und insgesamt fünf gewonnenen Sätzen nur den 3. Platz erreicht. Jemand muss ja ansonsten auch mal verlieren – diesmal war es der Spieler Nr. A.
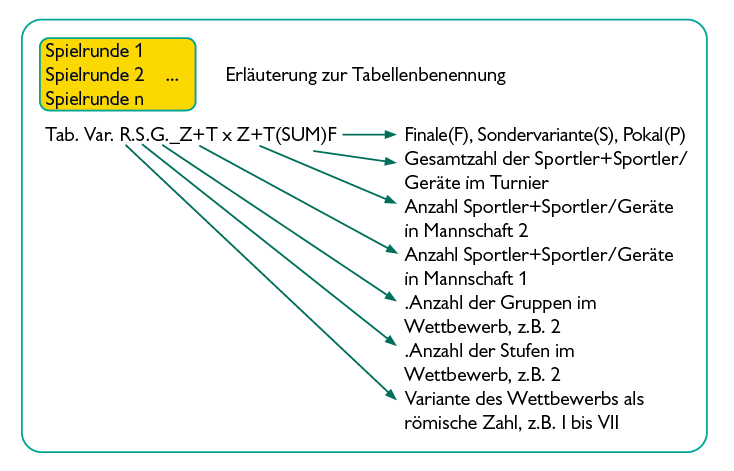
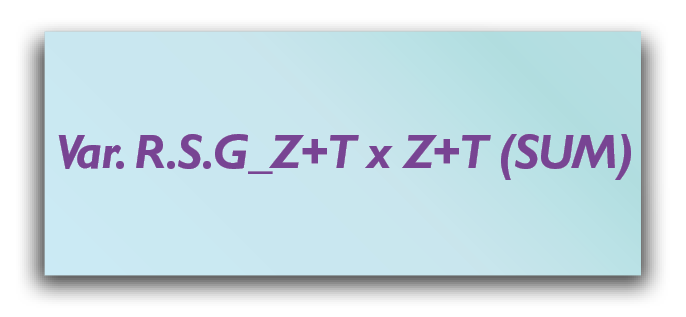
wobei
- R eine römische Bezeichnung der jeweiligen op-tc-Variante ist (z. B. von I bis VII)
- S ist die Anzahl der Stufen im Wettbewerb (z. B. von 1 bis 5)
- G stellt die Anzahl der Gruppen in der 1. Stufe dar (z. B. von 1 bis 10)
- Z ist die Teilnehmerzahl in der Einheit (im Team) + T als Torwart oder Tier/Gerät der Mannschaften 1 und 2 (z. B. von 1 bis 10 + 1 bis 2).
- In Klammern wird SUM als die Gesamtsumme der Mitspieler (z. B. von 3 bis 20+4) angegeben.
Noch ein Beispiel zur Relation der Einzel- und Mannschafts-Ergebnisse:
2. Tanzturnier-Weltmeisterschaft
Das Tanzpaar Deutschland (Partner 1GER und Dame DGER) tanzt im Finale der Tango-Weltmeisterschaft gegen die Paare der Länder Russland (Partner 2RUS und Dame
RRUS) und Italien (Partner 3ITA und Dame IITA).
Also 1GER DGER ⇔ 2RUS RRUS ⇔ 3ITA IITA– 3 Tanzpaare stehen im Wettbewerb.
Angenommen das gesellschaftliche Ergebnis des Länderwettbewerbs ist z. B.:

1. Platz – Russland,
2. Platz – Deutschland,
3. Platz – Italien.
Tango-Weltmeisterschaft, Turnierergebnis:
Das Tanzpaar
2RUS RRUS belegt das oberste Treppchen
1GER DGER – 2. Platz
3ITA IITA – 3. Platz
Insbesondere in Sportarten, deren subjektive Wertung vom künstlerischen Ausdruck und der technischen Perfektion abhängt, können durch andere Partner-Zusammensetzung sogar eher abweichende Resultate erzielt werden. Ein mögliches rechnerisches Ergebnis könnte nach einer Rotation der Einzeltänzer in den Tanzpaaren vielleicht so aussehen:
Ergebnis bei teamübergreifender Rotation, z. B.:
Das Tanzpaar
2RUS DGER belegt das oberste Treppchen
1GER IITA – 2. Platz
3ITA RRUS – 3. Platz
In diesem Fall ist die Weltmeisterin aus Russland rechnerisch auf den 3. Platz gerückt! Obwohl es nur ein Beispiel ist, kann das Ergebnis durchaus realistisch sein.
Es muss ja nicht unbedingt ein für die Ehre eines Landes so entscheidendes Beispiel sein.
Das geschilderte Prinzip könnte auf Sportwettbewerbe jeglicher Art zutreffen – angefangen von Kindermannschaften bis zu Turnieren in den obersten Ligen. Gegenwärtig wird die zweite in den Beispielen geschilderte individuellere Möglichkeit der Gestaltung eines Wettbewerbs meistens außer Acht gelassen.

Was schade ist, da manchmal Personen, die nicht so „mannschaftsgebunden“, sondern mehr „mannschaftsorientiert“ sind, die Chance sich in dieser zweiten, „mannschaftsunabhängigen“ Richtung zu entwickeln nicht haben.
Für Mannschaftskämpfe können die bestehenden, heute existierenden Wettbewerbsregeln im Sport, in der Unterhaltung und teilweise in der Kultur und Kunst, so zusammengefasst werden:

Vorgeschlagene Alternative zu dem heutigen Stand in den Wettbewerben ist die

Die Grundformulierung dieses neu ausgearbeiteten Prinzips der mathematischen Vorgänge, in diesem Fall der Gestaltung von Turnieren, Wettbewerben, Veranstaltungen lautet:



In einer einfachen und viel praktischeren und zugänglicheren Form findet man in der heutigen Welt die Umsetzung des als Alternative vorgestellten Prinzips nicht.
